The following is a concrete example to understand. As shown in the figure, in a nine-box diagram, the green position represents the starting position, the red position represents the end position, the gray area and the border of the box diagram represents this road is not available, please move from the starting position to the end position in accordance with the method that only one frame can be moved at a time.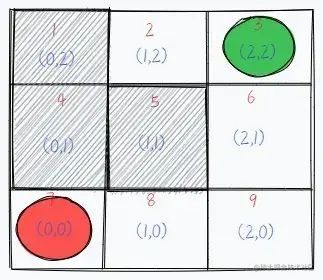

We use the DFS method to solve this problem, from the figure can be seen, we can go up and down, left and right four directions, we may first agree to “left > up > right > down” order to go, that is, if the left can go, we first go left. Then “recursive” down, did not reach the end, we then return to the original way, and so back to this position, the left has gone, then we go above, in this order. And we mark the way we went (direction) as “no going back”.

According to the agreement, we first from the starting point first to the left to go to position 2, then found that the left can not go, then we consider going up, found that also can not go, the same way, the lower side can not go. The right side has just gone also can not go, this time there is no way to go, on behalf of the road can not lead to the end, so now “no way to go”, along the original road back until you return to the intersection of the road that has not been taken, try to continue to take the path not taken.

So we have to go back to the initial position 1, and then judge the left has just gone and confirmed that this direction does not work, then do not have to go, the upper and right is also not possible, so we go down. So we went to the position of 6, at this time or in accordance with the agreement “left > up > right > down” order to go, the left and right still can not, the upper side has just gone, so we have to continue to go down.

Continue down that is the position 9, to this junction we continue to follow the agreed “left > up > right > down” order, first to the left found that you can go, then continue to go to position 8, to position 8 or continue to the left in accordance with the earlier thinking, found that you can still go, and finally reach the end of position 7.

In summary, this process is “depth-first traversal”.

The focus of DFS is on state backtracking，So let’s summarize our thoughts：

  • Depth-first traversal Keeps going as long as there is a path ahead that can be followed, and does not turn back until there is no more path to follow.

  • There are two cases of “no way out”: ① encountering a wall; ② encountering a road that has already been traveled.

  • When there is “no way out,” go back the way you came until you come back to the intersection where there is an untraveled path, and try to continue on the untraveled path.

  • There are some paths that are not taken, this is because the exit is found and the program stops.

  • “Depth-first traversal” is also called “depth-first search”, where traversal is the description of behavior and search is the purpose (use).

  • Iteration is not a very profound thing, looking at all possible cases before you can say “target element found” or “target element not found”. It is also called exhaustive enumeration. Although the idea of exhaustive enumeration seems insignificant to humans, with the powerful computing power of computers, exhaustive enumeration can help us solve many problems that cannot be solved by specialized knowledge.

The code that uses DFS to answer the question is as follows：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
//We take the red dot position as coordinates {0,0} and the green position as coordinates {2,2}
//Coordinate position of the target
let target = {
  x: 0,
  y: 0
};
//Coordinate position of the green starting point
let currentLocation = {
  x: 2,
  y: 2
};
let used = []; //Used to mark which points on the map are traveled
let reached = false; //Whether the target location can be reached
// The grid indicating the gray area
const illegalLocation = [
  { x: 0, y: 2 }, //Coordinates of serial number 1
  { x: 0, y: 1 }, //Coordinates of serial number 4
  { x: 1, y: 1 } //Coordinates of serial number 5
];

function isLegalLocation({ x, y }, illegalLocation) {
  let flag = true;
  //Location cannot be outside the map coordinates
  if (x < 0 || x > 2 || y < 0 || y > 2) {
    return (flag = false);
  }
  //The path that cannot be taken
  for (const { x: locX, y: locY } of illegalLocation) {
    if (x === locX && y === locY) {
      flag = false;
    }
  }
  return flag;
}

//Move to the left
function toLeft({ x, y }) {
  return { x: x - 1, y };
}

//Move up
function toTop({ x, y }) {
  return { x, y: y + 1 };
}

//Move right
function toRight({ x, y }) {
  return { x: x + 1, y };
}

//Move down
function toBottom({ x, y }) {
  return { x, y: y - 1 };
}

function dfs(target, location, illegalLocation, used) {
  // If the current position is the same as the target coordinates, it means that it can be reached
  if (Object.entries(target).toString() === Object.entries(location).toString()) {
    console.log('reached', location);
    return (reached = true);
  }
  let current = location;
  const newIllegalLocation = illegalLocation.concat(used);
  //Assuming the order of "left > top > right > bottom"
  if (isLegalLocation(toLeft(location), newIllegalLocation)) {
    current = toLeft(location);
  } else if (isLegalLocation(toTop(location), newIllegalLocation)) {
    current = toTop(location);
  } else if (isLegalLocation(toRight(location), newIllegalLocation)) {
    current = toRight(location);
  } else if (isLegalLocation(toBottom(location), newIllegalLocation)) {
    current = toBottom(location);
  } else {
     //If you can't go, just go back
    return false
  }
  used.push(current); //Mark the grid you just walked on as walked
  return dfs(target, current, illegalLocation, used); //Recursion goes on
}

dfs(target, currentLocation, illegalLocation, used);

The difference between BFS and DFS is that BFS aims to write down all the forks when facing an intersection, then select one to enter, then record its diversion, then return to enter another fork and repeat the operation, which is represented graphically as follows.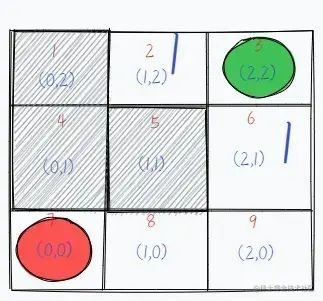

From the green starting point, record all the forks in the road and mark them as reachable by taking one step. Then choose one of the directions to walk into, we take the one to the left of the green (serial number 2) grid, and then record and mark this intersection as a walkable direction of 2, meaning a place that can be reached by taking two steps.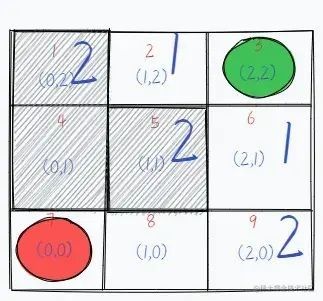

Next, we go back to the square 1 below the starting point (serial number 6) and record the direction it can go, also marked as 2, because it is also a place that can be reached in two steps. This way, we can search for places that can be reached in one step and in two steps, and then we can mark the squares that can be reached in three steps.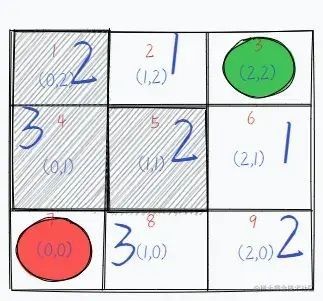

This is followed by the fourth step. We then successfully find the path and find all feasible paths.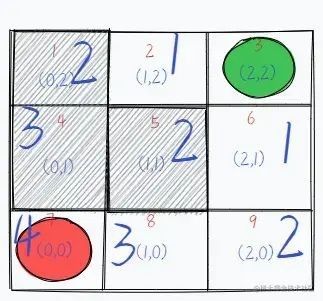

Note: The gray areas where the grid serial numbers are 1, 4 and 5 respectively indicate that the path is not available.

The code for using BFS to answer the question just asked is as follows.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
//We take the red dot position as coordinates {0,0} and the green position as coordinates {2,2}
//Coordinate position of the target
let target = {
  x: 0,
  y: 0
};
//Coordinate position of the green starting point
let currentLocation = {
  x: 2,
  y: 2
};
// The grid indicating the gray area
const illegalLocation = [
  { x: 0, y: 2 }, //Coordinates of serial number 1
  { x: 0, y: 1 }, //Coordinates of serial number 4
  { x: 1, y: 1 }, //Coordinates of serial number 5
];

function isLegalLocation({ x, y }, illegalLocation) {
  let flag = true;
  //Location cannot be outside the map coordinates
  if (x < 0 || x > 2 || y < 0 || y > 2) {
    return (flag = false);
  }
  //The path that cannot be taken
  for (const { x: locX, y: locY } of illegalLocation) {
    if (x === locX && y === locY) {
      flag = false;
    }
  }
  return flag;
}

//Move to the left
function toLeft({ x, y }) {
  return { x: x - 1, y };
}

//Move up
function toTop({ x, y }) {
  return { x, y: y + 1 };
}

//Move to the right
function toRight({ x, y }) {
  return { x: x + 1, y };
}

//Move down
function toBottom({ x, y }) {
  return { x, y: y - 1 };
}

function search(location, illegalLocation) {
  let locations = new Set()
  //Assuming the order of "left > top > right > bottom"
  if (isLegalLocation(toLeft(location), illegalLocation)) {
    locations.add(toLeft(location))
  } 
  if (isLegalLocation(toTop(location), illegalLocation)) {
    locations.add(toTop(location))
  }
  if (isLegalLocation(toRight(location), illegalLocation)) {
    locations.add(toRight(location))
  }
  if (isLegalLocation(toBottom(location), illegalLocation)) {
    locations.add(toBottom(location))
  }
  return locations
}

function bfs(target, location, illegalLocation) {
  let reached = false; //Whether the target location can be reached
  let stack = [];  
  let searched = new Set() //Already walked the grid
  stack.push(location);
  while(stack.length) {
    const current = stack.shift()
    const newIllegalLocation = illegalLocation.concat([...searched]);
    //First seen first traversed
    const searchedSet = search(current, newIllegalLocation)
    Array.from(searchedSet).forEach((el) => {
      searched.add(el)
    })
    for (const { x: locX, y: locY } of searchedSet) {
      stack.push({ x: locX, y: locY })
      if (target.x === locX && target.y === locY) {
        //If the current position is the same as the target coordinates, it means that it can be reached
        reached = true;
        console.log('reached: ', reached);
        stack = [];
        break;
      }
    }
  }
  return reached;
}
bfs(target, currentLocation, illegalLocation);

The idea of “breadth-first traversal” can be found everywhere in life.

  • If we were looking for a lawyer, we would first look among our friends, and if we didn’t find one, continue to look among our friends’ friends until we found one.
  • When a stone is thrown into the calm water, the ripples caused by one layer are characterized by “breadth-first traversal”.
Summary
  • The most intuitive description of DFS is “one way to the end, no turning back until you hit the south wall”. So DFS can be implemented with “recursion”.
  • BFS has a “layer-by-layer outward expansion” feature, where the nodes seen first are traversed first and the nodes seen later are traversed later, so BFS can be implemented with the help of a “queue”. (When traversing a node, if it has left (right) children, add them to the queue in turn.)
  • DFS is good for targeted searches, while BFS is good for large scale searches.